1. Mục tiêu
- Hiểu được tư tưởng cốt lõi của thuật toán quay lui: tìm kiếm theo chiều sâu trong không gian trạng thái và quay lại khi gặp ngõ cụt.
- Nắm vững cách áp dụng quay lui để giải quyết các bài toán duyệt và liệt kê cấu hình, điển hình là bài toán N quân hậu và bài toán liệt kê hoán vị.
- Cài đặt được thuật toán quay lui bằng kỹ thuật đệ quy trong Python.
2. Bài toán dẫn nhập
Xét bài toán: Liệt kê tất cả các hoán vị của tập hợp ba số {1, 2, 3}.
Một hoán vị là một cách sắp xếp các phần tử. Bằng phương pháp thủ công, ta có thể dễ dàng liệt kê được 6 hoán vị: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
Tuy nhiên, làm thế nào để máy tính có thể tự động sinh ra tất cả các kết quả này một cách có hệ thống? Ta có thể hình dung quá trình xây dựng một hoán vị theo từng bước:
- Chọn phần tử đầu tiên:
- Thử chọn số 1. Cấu hình hiện tại là (1, …).
- Tiếp theo, ta cần chọn phần tử thứ hai từ các số còn lại {2, 3}.
- Chọn phần tử thứ hai:
- Thử chọn số 2. Cấu hình hiện tại là (1, 2, …).
- Số còn lại là {3}. Ta chọn số 3.
- Chọn phần tử thứ ba:
- Ta chọn số 3. Cấu hình hoàn chỉnh là (1, 2, 3). Đây là một kết quả.
- Không còn lựa chọn nào khác ở bước này. Ta phải quay lại bước 2.
- Quay lại bước 2:
- Ta đã thử chọn số 2. Bây giờ ta thử lựa chọn còn lại là số 3. Cấu hình hiện tại là (1, 3, …).
- Số còn lại là {2}. Ta chọn số 2.
- Chọn phần tử thứ ba (lần 2):
- Ta chọn số 2. Cấu hình hoàn chỉnh là (1, 3, 2). Đây là một kết quả.
- Không còn lựa chọn nào khác. Ta quay lại bước 2.
- Quay lại bước 2 (lần 2):
- Ta đã thử hết các lựa chọn (2 và 3). Không còn cách nào để đi tiếp. Ta phải quay lại bước 1.
- Quay lại bước 1:
- Ta đã thử chọn số 1 cho vị trí đầu tiên. Bây giờ ta thử chọn số 2. Cấu hình hiện tại là (2, …).
Quá trình này tiếp tục cho đến khi tất cả các lựa chọn ở bước 1 (chọn 1, 2, hoặc 3) đều được khám phá hết. Tư tưởng “thử một lựa chọn, đi sâu vào giải quyết phần còn lại, và nếu không thành công hoặc đã khám phá hết thì quay lại để thử lựa chọn khác” chính là cốt lõi của thuật toán quay lui.
3. Nguyên lý thuật toán
3.1. Ý tưởng cốt lõi
Quay lui (Backtracking) là một kỹ thuật thuật toán dùng để giải quyết các bài toán bằng cách xây dựng dần các ứng viên cho lời giải và loại bỏ những ứng viên không thỏa mãn điều kiện ngay khi có thể.
Thuật toán hoạt động dựa trên nguyên tắc của tìm kiếm theo chiều sâu (Depth-First Search – DFS) trên một không gian các trạng thái. Không gian này thường được biểu diễn dưới dạng một cây, gọi là cây trạng thái (state-space tree), trong đó:
- Gốc cây biểu diễn trạng thái ban đầu (chưa có lựa chọn nào).
- Mỗi nút trong cây biểu diễn một trạng thái, tức một cấu hình đang được xây dựng dở dang.
- Các cạnh nối từ một nút cha đến các nút con biểu diễn các lựa chọn có thể thực hiện để mở rộng cấu hình từ trạng thái cha.
- Các nút lá biểu diễn các cấu hình đã xây dựng xong (có thể là lời giải hoặc không).
Quá trình quay lui sẽ duyệt cây trạng thái này. Khi đi xuống một nhánh, thuật toán đang “thử” một chuỗi các lựa chọn. Nếu tại một nút, thuật toán phát hiện ra rằng nhánh này không thể dẫn đến một lời giải hợp lệ, nó sẽ không đi sâu hơn nữa mà “quay lui” lên nút cha và thử một nhánh khác.
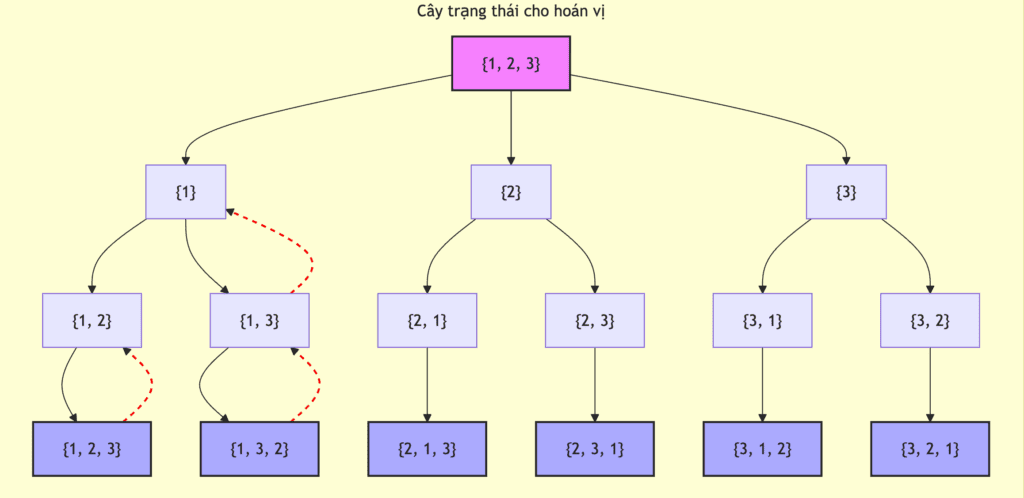
3.2. Minh họa các bước thực thi
Sử dụng lại bài toán liệt kê hoán vị của {1, 2, 3}, cây trạng thái được duyệt như sau:
4. Cài đặt thuật toán
Thuật toán quay lui thường được cài đặt một cách tự nhiên bằng đệ quy. Một hàm đệ quy quay lui điển hình có cấu trúc như sau:
def backtrack(candidate):
# Trường hợp cơ sở: nếu candidate là một lời giải hoàn chỉnh
if is_a_solution(candidate):
process_solution(candidate)
return
# Duyệt qua tất cả các lựa chọn tiếp theo có thể
for next_choice in generate_next_choices(candidate):
# 1. Thử lựa chọn
add_to_candidate(next_choice, candidate)
# 2. Gọi đệ quy để đi sâu hơn
backtrack(candidate)
# 3. Quay lui: xóa lựa chọn vừa thử để thử lựa chọn khác
remove_from_candidate(next_choice, candidate)Ví dụ cài đặt cho bài toán liệt kê hoán vị:
def find_permutations(nums):
"""
Hàm chính khởi tạo và gọi hàm đệ quy quay lui.
"""
def backtrack(current_permutation, remaining_nums):
"""
Hàm đệ quy thực hiện quay lui.
- current_permutation: hoán vị đang được xây dựng
- remaining_nums: tập các số chưa được sử dụng
"""
# Trường hợp cơ sở: nếu không còn số nào để chọn,
# ta đã có một hoán vị hoàn chỉnh.
if not remaining_nums:
result.append(list(current_permutation))
return
# Duyệt qua các số còn lại để thử cho vị trí tiếp theo
for i in range(len(remaining_nums)):
num = remaining_nums[i]
# 1. Thử: Thêm số được chọn vào hoán vị hiện tại
current_permutation.append(num)
# Tạo danh sách các số còn lại mới
new_remaining = remaining_nums[:i] + remaining_nums[i+1:]
# 2. Đệ quy: Gọi lại hàm với trạng thái mới
backtrack(current_permutation, new_remaining)
# 3. Quay lui: Xóa số vừa thêm để thử các lựa chọn khác
current_permutation.pop()
result = []
backtrack([], nums)
return result
# Chạy chương trình
numbers = [1, 2, 3]
permutations = find_permutations(numbers)
print(permutations)
# Kết quả: [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]5. Trực quan hóa và gỡ lỗi với Thonny
Môi trường lập trình Thonny là một công cụ hữu ích để hiểu rõ cách hoạt động của đệ quy và quay lui. Bằng cách sử dụng trình gỡ lỗi (debugger) của Thonny, học sinh có thể theo dõi từng bước của thuật toán:
- Chép đoạn mã nguồn trên vào Thonny.
- Chọn Run -> Debug current script (hoặc nhấn Ctrl+F5).
- Sử dụng nút Step into (F7) để đi vào bên trong các lời gọi hàm backtrack.
- Quan sát cửa sổ Call stack (ngăn xếp lời gọi). Mỗi lần hàm backtrack được gọi, một frame mới sẽ được thêm vào ngăn xếp. Khi một lời gọi hàm kết thúc (return), frame tương ứng sẽ được xóa khỏi ngăn xếp – đây chính là hành động “quay lui” được trực quan hóa.
- Theo dõi sự thay đổi của các biến
current_permutationvàremaining_numstrong cửa sổ Variables để thấy rõ quá trình xây dựng và hủy bỏ các cấu hình.
6. Bài tập vận dụng
6.1. Đề bài: Bài toán N quân hậu (N-Queens)
Đặt N quân hậu trên một bàn cờ vua kích thước N×N sao cho không có hai quân hậu nào có thể ăn nhau. Điều này có nghĩa là không có hai quân hậu nào được đặt trên cùng một hàng, cùng một cột, hoặc cùng một đường chéo.
Yêu cầu: Liệt kê tất cả các cách đặt N quân hậu thỏa mãn.
6.2. Lời giải và phân tích
Phân tích:
- Không gian trạng thái: Mỗi trạng thái là một cách đặt k quân hậu trên k hàng đầu tiên (mỗi hàng một quân) sao cho chúng không ăn nhau.
- Xây dựng lời giải: Ta sẽ đặt các quân hậu lần lượt vào các hàng, từ hàng 0 đến hàng N-1. Tại mỗi hàng, ta thử đặt quân hậu vào từng cột, từ cột 0 đến cột N-1.
- Điều kiện ràng buộc: Trước khi đặt một quân hậu vào vị trí
(row, col), ta phải kiểm tra xem vị trí này có bị các quân hậu đã đặt ở các hàng trước đó tấn công hay không (kiểm tra cột, đường chéo chính, và đường chéo phụ). - Quay lui: Nếu ta đã thử hết các cột trong một hàng mà không tìm được vị trí hợp lệ, ta phải quay lui về hàng trước đó, di chuyển quân hậu ở hàng đó sang một cột khác và tiếp tục.
Cài đặt:
def solve_n_queens(n):
"""
Hàm giải bài toán N quân hậu.
"""
def is_safe(board, row, col):
"""
Kiểm tra xem việc đặt hậu tại board[row][col] có an toàn không.
Ta chỉ cần kiểm tra các hàng phía trên.
"""
# Kiểm tra cột
for i in range(row):
if board[i] == col:
return False
# Kiểm tra đường chéo trên bên trái
i, j = row - 1, col - 1
while i >= 0 and j >= 0:
if board[i] == j:
return False
i, j = i - 1, j - 1
# Kiểm tra đường chéo trên bên phải
i, j = row - 1, col + 1
while i >= 0 and j < n:
if board[i] == j:
return False
i, j = i - 1, j + 1
return True
def backtrack(row):
"""
Hàm đệ quy quay lui để đặt hậu từ hàng 'row'.
"""
# Trường hợp cơ sở: nếu đã đặt hậu cho tất cả các hàng
if row == n:
# Xây dựng và lưu lại một lời giải từ mảng board
solution = []
for r in range(n):
line = "*" * board[r] + "Q" + "*" * (n - board[r] - 1)
solution.append(line)
result.append(solution)
return
# Duyệt qua tất cả các cột trong hàng hiện tại
for col in range(n):
# Nếu vị trí (row, col) là an toàn
if is_safe(board, row, col):
# 1. Thử: đặt hậu vào vị trí này
board[row] = col
# 2. Đệ quy: giải quyết cho hàng tiếp theo
backtrack(row + 1)
# 3. Quay lui: không cần thực hiện tường minh vì ở vòng lặp
# tiếp theo, board[row] sẽ được gán giá trị mới.
# board[i] = c nghĩa là quân hậu ở hàng i được đặt ở cột c
board = [-1] * n
result = []
backtrack(0)
return result
# Chạy chương trình với N = 4
n = 4
solutions = solve_n_queens(n)
for i, sol in enumerate(solutions):
print(f"Solution {i+1}:")
for row_str in sol:
print(row_str)
print("-" * 10)7. Đánh giá thuật toán và mở rộng
7.1. Phân tích độ phức tạp
Độ phức tạp của thuật toán quay lui rất khó để phân tích chính xác và thường phụ thuộc nhiều vào bài toán cụ thể và các kỹ thuật cắt tỉa (pruning).
Nhìn chung, độ phức tạp trong trường hợp xấu nhất là hàm số của số nút trong cây trạng thái. Đối với bài toán N quân hậu, một ước lượng thô cho độ phức tạp là O(N!), vì ở hàng đầu tiên có N lựa chọn, hàng thứ hai có khoảng N-1 lựa chọn, v.v.
Thuật toán quay lui hiệu quả hơn duyệt toàn bộ vì nó cắt bỏ các nhánh không tiềm năng từ sớm.
7.2. Các trường hợp đặc biệt và biến thể
Quay lui là một kỹ thuật rất mạnh và có thể áp dụng cho nhiều lớp bài toán khác nhau, bao gồm:
- Bài toán thỏa mãn ràng buộc (Constraint Satisfaction Problems): Ví dụ như giải Sudoku.
- Bài toán liệt kê: Liệt kê các tổ hợp, chỉnh hợp.
- Bài toán tìm đường đi: Tìm đường đi trong mê cung.
8. Tổng kết
- Quay lui là một chiến lược giải quyết vấn đề dựa trên việc xây dựng lời giải từng bước và quay lại khi một bước đi dẫn đến ngõ cụt.
- Nó được cài đặt một cách hiệu quả và tự nhiên bằng đệ quy.
- Cấu trúc cốt lõi của một hàm quay lui bao gồm ba bước: Thử (Try), Đệ quy (Recurse), và Quay lui (Backtrack).
- Đây là một thuật toán nền tảng cho nhiều bài toán tìm kiếm và tối ưu hóa trong lập trình.



