Ôn thi HSG Tin học THPT – Bài 13: Lý thuyết số - Phần 1

1. Mục tiêu

Trình bày và cài đặt được các phương pháp cơ bản để kiểm tra tính nguyên tố của một số nguyên dương.
Nắm vững các khái niệm toán học nền tảng: ước số, bội số, ước chung lớn nhất (UCLN), và bội chung nhỏ nhất (BCNN).
Hiểu rõ và cài đặt được Thuật toán Euclid để tìm UCLN một cách hiệu quả.
Áp dụng các kiến thức trên để giải quyết các bài toán liên quan.

2. Bài toán dẫn nhập

Xét bài toán: Cho hai số nguyên dương a và b có giá trị rất lớn (ví dụ, lên tới 10¹⁸). Cần tìm ước chung lớn nhất của chúng.

Một phương pháp tự nhiên là duyệt qua tất cả các số từ min(a, b) trở xuống và kiểm tra xem số đó có phải là ước chung của a và b hay không. Số đầu tiên tìm được sẽ là UCLN. Tuy nhiên, với dữ liệu lớn, phương pháp này đòi hỏi một lượng phép tính khổng lồ và không thể hoàn thành trong giới hạn thời gian cho phép của các kỳ thi. Điều này đặt ra yêu cầu phải có một thuật toán hiệu quả hơn, và Thuật toán Euclid chính là giải pháp cho vấn đề này.

3. Nguyên lý thuật toán

3.1. Các khái niệm cơ bản

3.1.1. Ước số và Bội số

Số nguyên a được gọi là ước số (hay thừa số) của số nguyên b nếu tồn tại số nguyên k sao cho b = a * k. Khi đó, b được gọi là bội số của a.
Ví dụ: 3 là ước của 12, vì 12 = 3 * 4. Ngược lại, 12 là bội của 3.

3.1.2. Số nguyên tố

Số nguyên tố là số tự nhiên lớn hơn 1 và chỉ có hai ước số dương là 1 và chính nó.
Ví dụ: 2, 3, 5, 7, 11, 13 là các số nguyên tố. Số 4 không phải là số nguyên tố vì có ước là 2. Số 1 không phải là số nguyên tố.

3.1.3. Ước chung lớn nhất (UCLN) và Bội chung nhỏ nhất (BCNN)

Ước chung lớn nhất (UCLN) của hai hay nhiều số nguyên là số nguyên dương lớn nhất là ước số của tất cả các số đó. Ký hiệu: UCLN(a, b) hoặc GCD(a, b).
Bội chung nhỏ nhất (BCNN) của hai hay nhiều số nguyên là số nguyên dương nhỏ nhất là bội số của tất cả các số đó. Ký hiệu: BCNN(a, b) hoặc LCM(a, b).
Mối quan hệ quan trọng giữa UCLN và BCNN của hai số nguyên dương a và b được thể hiện qua công thức: UCLN(a, b) * BCNN(a, b) = a * b.

3.2. Thuật toán kiểm tra số nguyên tố

3.2.1. Ý tưởng cốt lõi (Phương pháp duyệt ước số)

Để kiểm tra xem một số nguyên dương n > 1 có phải là số nguyên tố hay không, ta chỉ cần kiểm tra xem nó có chia hết cho bất kỳ số nguyên d nào trong khoảng 2 ≤ d < n hay không. Nếu không tìm thấy d nào, n là số nguyên tố.

Một cải tiến quan trọng là ta chỉ cần kiểm tra các ước số d trong khoảng 2 ≤ d ≤ sqrt(n). Lý do là nếu n có một ước số d1 > sqrt(n), thì nó cũng phải có một ước số d2 = n / d1. Dễ thấy rằng d2 < sqrt(n). Do đó, nếu n có ước lớn hơn sqrt(n) thì chắc chắn nó cũng có ước nhỏ hơn sqrt(n). Vì vậy, chỉ cần kiểm tra đến sqrt(n) là đủ.

3.2.2. Minh họa các bước thực thi

Xét n = 29.

Tính sqrt(29) ≈ 5.38. Ta cần kiểm tra các ước số từ 2 đến 5.
29 % 2 != 0.
29 % 3 != 0.
29 % 4 != 0.
29 % 5 != 0.
Kết thúc vòng lặp. Không tìm thấy ước số nào trong khoảng [2, 5]. Kết luận: 29 là số nguyên tố.

3.3. Thuật toán Euclid

3.3.1. Ý tưởng cốt lõi

Thuật toán Euclid dựa trên một nguyên lý cơ bản: Ước chung lớn nhất của hai số a và b (giả sử a ≥ b) cũng chính là ước chung lớn nhất của b và phần dư của a cho b.
UCLN(a, b) = UCLN(b, a % b)

Thuật toán lặp lại quá trình này cho đến khi một trong hai số bằng 0. Khi đó, UCLN chính là số còn lại. Cụ thể, nếu b = 0, thì UCLN(a, 0) = a.

3.3.2. Minh họa các bước thực thi

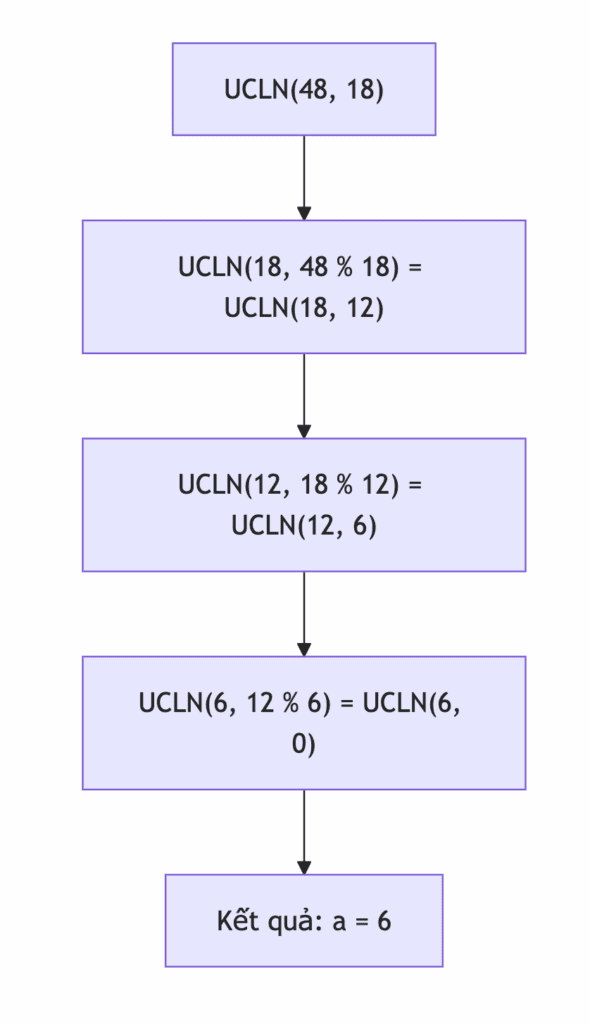
Tìm UCLN(48, 18):

UCLN(48, 18) = UCLN(18, 48 % 18) = UCLN(18, 12)
UCLN(18, 12) = UCLN(12, 18 % 12) = UCLN(12, 6)
UCLN(12, 6) = UCLN(6, 12 % 6) = UCLN(6, 0)
Gặp trường hợp cơ sở (b=0). Kết quả là a = 6.
Vậy, UCLN(48, 18) = 6.

4. Cài đặt thuật toán

import math

def is_prime(n):
    """
    Kiểm tra xem một số nguyên dương n có phải là số nguyên tố hay không.
    Sử dụng phương pháp duyệt ước số tới căn bậc hai của n.
    """
    if n < 2:
        return False  # Các số nhỏ hơn 2 không phải là số nguyên tố
    
    # Duyệt các số từ 2 đến căn bậc hai của n
    for i in range(2, int(math.sqrt(n)) + 1):
        if n % i == 0:
            return False  # Nếu n chia hết cho i, n không phải số nguyên tố
            
    return True # Nếu không tìm thấy ước nào, n là số nguyên tố

def gcd(a, b):
    """
    Tìm ước chung lớn nhất (UCLN) của hai số a và b bằng thuật toán Euclid (dạng đệ quy).
    """
    if b == 0:
        return a # Trường hợp cơ sở của đệ quy
    else:
        return gcd(b, a % b) # Bước đệ quy

def lcm(a, b):
    """
    Tìm bội chung nhỏ nhất (BCNN) của hai số a và b dựa vào công thức
    LCM(a, b) = (a * b) / GCD(a, b).
    """
    if a == 0 or b == 0:
        return 0
    # Sử dụng phép chia số nguyên (//) để đảm bảo kết quả là số nguyên
    return abs(a * b) // gcd(a, b)

5. Trực quan hóa và gỡ lỗi với Thonny

Để hiểu rõ cách Thuật toán Euclid hoạt động, đặc biệt là phiên bản đệ quy, việc sử dụng trình gỡ lỗi (debugger) của Thonny là vô cùng hữu ích.

Mở Thonny và dán đoạn mã của hàm gcd vào.
Thêm một dòng lệnh gọi hàm, ví dụ: print(gcd(48, 18)).
Đặt một điểm dừng (breakpoint) tại dòng if b == 0:.
Chạy chương trình ở chế độ gỡ lỗi (Debug current script).
Sử dụng nút “Step Into” để đi sâu vào từng lời gọi đệ quy. Quan sát cửa sổ “Call stack” để thấy các lời gọi hàm gcd được xếp chồng lên nhau như thế nào, và theo dõi sự thay đổi của các biến cục bộ a và b trong mỗi lời gọi.

6. Bài tập vận dụng

6.1. Đề bài

Viết chương trình cho phép nhập vào hai phân số dưới dạng a/b và c/d. Tính tổng của hai phân số này và in kết quả ra màn hình dưới dạng phân số tối giản.

6.2. Lời giải và phân tích

Phân tích thuật toán:

Công thức cộng hai phân số a/b và c/d là: (a*d + c*b) / (b*d).
Kết quả thu được là một phân số mới, có tử số là tu_moi = a*d + c*b và mẫu số là mau_moi = b*d.
Để tối giản phân số này, ta cần tìm UCLN của tử số và mẫu số mới: ucln = UCLN(tu_moi, mau_moi).
Phân số tối giản cuối cùng sẽ có tử số là tu_moi / ucln và mẫu số là mau_moi / ucln.

Cài đặt:

def gcd(a, b):
    """
    Tìm ước chung lớn nhất (UCLN) của hai số a và b bằng thuật toán Euclid.
    """
    while b:
        a, b = b, a % b
    return a

# Nhập dữ liệu cho phân số thứ nhất
a, b = map(int, input("Nhập phân số thứ nhất (a/b): ").split('/'))

# Nhập dữ liệu cho phân số thứ hai
c, d = map(int, input("Nhập phân số thứ hai (c/d): ").split('/'))

# Tính tử số và mẫu số của tổng
tu_so_tong = a * d + c * b
mau_so_tong = b * d

# Tìm UCLN để tối giản phân số
common_divisor = gcd(tu_so_tong, mau_so_tong)

# Tối giản tử số và mẫu số
tu_so_toi_gian = tu_so_tong // common_divisor
mau_so_toi_gian = mau_so_tong // common_divisor

# In kết quả
print(f"Tổng hai phân số là: {tu_so_toi_gian}/{mau_so_toi_gian}")

7. Đánh giá thuật toán và mở rộng

7.1. Phân tích độ phức tạp

Kiểm tra số nguyên tố: Thuật toán duyệt ước số có độ phức tạp thời gian là O(sqrt(n)), vì vòng lặp chạy tối đa sqrt(n) lần.
Thuật toán Euclid: Độ phức tạp thời gian của thuật toán này là O(log(min(a, b))). Điều này là do sau mỗi hai bước đệ quy, giá trị của các tham số giảm ít nhất một nửa, dẫn đến độ phức tạp dạng logarithmic, cực kỳ hiệu quả.

7.2. Các trường hợp đặc biệt và biến thể

Kiểm tra số nguyên tố: Cần xử lý các trường hợp đặc biệt n < 2. Các thuật toán kiểm tra nguyên tố hiệu quả hơn như sàng Eratosthenes (khi cần tìm nhiều số nguyên tố trong một khoảng) hoặc các kiểm tra xác suất như Miller-Rabin sẽ được giới thiệu trong các bài học nâng cao.
Thuật toán Euclid mở rộng: Là một biến thể của thuật toán Euclid, không chỉ tìm UCLN của a và b mà còn tìm một cặp số nguyên x và y thỏa mãn phương trình Diophantine: a*x + b*y = UCLN(a, b).

8. Tổng kết

Bài học đã giới thiệu các khái niệm và thuật toán nền tảng trong lý thuyết số, một lĩnh vực quan trọng của toán học và khoa học máy tính. Các nội dung chính bao gồm:

Định nghĩa và phương pháp kiểm tra số nguyên tố.
Các khái niệm về ước số, bội số, UCLN và BCNN.
Nguyên lý và cách cài đặt Thuật toán Euclid, một giải pháp hiệu quả cho bài toán tìm UCLN.

Việc nắm vững các công cụ này là tiền đề cơ bản để giải quyết một lớp các bài toán rộng lớn trong lập trình thi đấu.