Ôn thi HSG Tin học THPT – Bài 14: Lý thuyết số – Phần 2 (Các dạng số đặc biệt)

1. Mục tiêu

  • Nắm được định nghĩa, tính chất và phương pháp kiểm tra một số nguyên dương có phải là số chính phương, số hoàn hảo, hay số Armstrong.
  • Làm quen với hai dãy số kinh điển trong toán học và khoa học máy tính: dãy Fibonacci và dãy số Catalan.
  • Hiểu và cài đặt được các công thức truy hồi hoặc công thức tính toán tổng quát cho các dãy số nêu trên bằng ngôn ngữ lập trình Python.
  • Rèn luyện kỹ năng chuyển hóa một định nghĩa toán học thành một thuật toán kiểm tra hoặc tính toán hiệu quả.

2. Giới thiệu và phạm vi ứng dụng

Lý thuyết số là một nhánh quan trọng trong lập trình thi đấu, cung cấp nền tảng để giải quyết nhiều bài toán phức tạp. Bên cạnh các khái niệm cơ bản như số nguyên tố hay ước chung lớn nhất, thế giới các con số còn tồn tại nhiều loại số đặc biệt với các tính chất toán học thú vị. Việc nhận biết và xử lý các dạng số này là một kỹ năng cần thiết.

Bài giảng này sẽ giới thiệu một số dạng số và dãy số đặc biệt thường gặp, bao gồm: Số chính phương, Số hoàn hảo, Số Armstrong, Dãy Fibonacci và Dãy số Catalan. Các khái niệm này không chỉ xuất hiện trong các bài toán lý thuyết số thuần túy mà còn có ứng dụng trong các lĩnh vực khác như quy hoạch động, tổ hợp và thuật toán.

3. Định nghĩa, thuộc tính và cài đặt

3.1. Số chính phương (Perfect Square)

3.1.1. Định nghĩa

Một số nguyên không âm n được gọi là số chính phương nếu nó là bình phương của một số nguyên k nào đó. n = k²
Ví dụ: 0, 1, 4, 9, 16, 25 là các số chính phương.

3.1.2. Phương pháp kiểm tra

Để kiểm tra một số nguyên n >= 0 có phải là số chính phương hay không, ta có thể thực hiện các bước sau:

  • Tính căn bậc hai của n: k = sqrt(n).
  • Làm tròn k xuống số nguyên gần nhất, ta được k_int = int(k).
  • Kiểm tra xem k_int * k_int có bằng n hay không. Nếu bằng, n là số chính phương.

3.1.3. Cài đặt

import math

def is_perfect_square(n: int) -> bool:
    """
    Kiểm tra một số nguyên không âm có phải là số chính phương hay không.
    
    Args:
        n: Số nguyên cần kiểm tra (n >= 0).
        
    Returns:
        True nếu n là số chính phương, False nếu không phải.
    """
    if n < 0:
        return False
    if n == 0:
        return True
    
    # Tính căn bậc hai và lấy phần nguyên
    sqrt_n = int(math.sqrt(n))
    
    # Kiểm tra bình phương của phần nguyên có bằng số ban đầu không
    return sqrt_n * sqrt_n == n

3.2. Số hoàn hảo (Perfect Number)

3.2.1. Định nghĩa

Một số nguyên dương n được gọi là số hoàn hảo nếu tổng các ước nguyên dương thực sự của nó (các ước không bao gồm chính nó) bằng chính nó.

Ví dụ: Số 6 có các ước thực sự là 1, 2, 3. Tổng các ước này là 1 + 2 + 3 = 6. Vậy 6 là một số hoàn hảo.

Ví dụ khác: 28 (có các ước 1, 2, 4, 7, 14; tổng là 28).

3.2.2. Phương pháp kiểm tra

Để kiểm tra một số nguyên dương n có phải là số hoàn hảo hay không, ta tính tổng các ước thực sự của nó và so sánh với n. Một cách hiệu quả để tìm tổng các ước là duyệt từ 1 đến sqrt(n).

3.2.3. Cài đặt với Python

def is_perfect_number(n: int) -> bool:
    """
    Kiểm tra một số nguyên dương có phải là số hoàn hảo hay không.
    Args:
        n: Số nguyên dương cần kiểm tra.
    Returns:
        True nếu n là số hoàn hảo, False nếu không phải.
    """
    if n <= 1:
        return False
    sum_of_divisors = 1 # Bắt đầu với 1 vì 1 luôn là ước
    
    # Duyệt tới căn bậc hai của n để tìm các cặp ước
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            sum_of_divisors += i
            # Nếu i không phải là căn bậc hai, cộng thêm ước tương ứng
            if i * i != n:
                sum_of_divisors += n // i
    return sum_of_divisors == n

3.3. Số Armstrong (Armstrong Number)

3.3.1. Định nghĩa

Một số Armstrong (hay còn gọi là số tự mãn) là một số mà giá trị của nó bằng tổng các lũy thừa bậc k của các chữ số của nó, với k là số lượng chữ số.

Ví dụ: Số 153 là một số Armstrong vì nó có 3 chữ số và 1³ + 5³ + 3³ = 1 + 125 + 27 = 153.

Ví dụ khác: 1634 (có 4 chữ số) vì 1⁴ + 6⁴ + 3⁴ + 4⁴ = 1 + 1296 + 81 + 256 = 1634.

3.3.2. Phương pháp kiểm tra

Đếm số lượng chữ số của n, đặt là k.

Khởi tạo một biến sum_of_powers = 0.

Tách từng chữ số của n, tính lũy thừa bậc k của chữ số đó và cộng vào sum_of_powers.

So sánh sum_of_powers với số n ban đầu.

3.3.3. Cài đặt với Python

def is_armstrong_number(n: int) -> bool:
    """
    Kiểm tra một số nguyên dương có phải là số Armstrong hay không.
    Args:
        n: Số nguyên dương cần kiểm tra.
    Returns:
        True nếu n là số Armstrong, False nếu không phải.
    """
    if n < 0:
        return False
    
    s = str(n)
    num_digits = len(s)
    sum_of_powers = 0
    
    for digit_char in s:
        digit = int(digit_char)
        sum_of_powers += digit ** num_digits
    
    return sum_of_powers == n

3.4. Dãy Fibonacci

3.4.1. Giới thiệu và công thức truy hồi

Dãy Fibonacci là dãy số trong đó mỗi số hạng (kể từ số hạng thứ ba) là tổng của hai số hạng đứng ngay trước nó.

  • Công thức truy hồi:
    • F(0) = 0
    • F(1) = 1
    • F(n) = F(n-1) + F(n-2) với n > 1

Dãy số bắt đầu: 0, 1, 1, 2, 3, 5, 8, 13, 21, ...

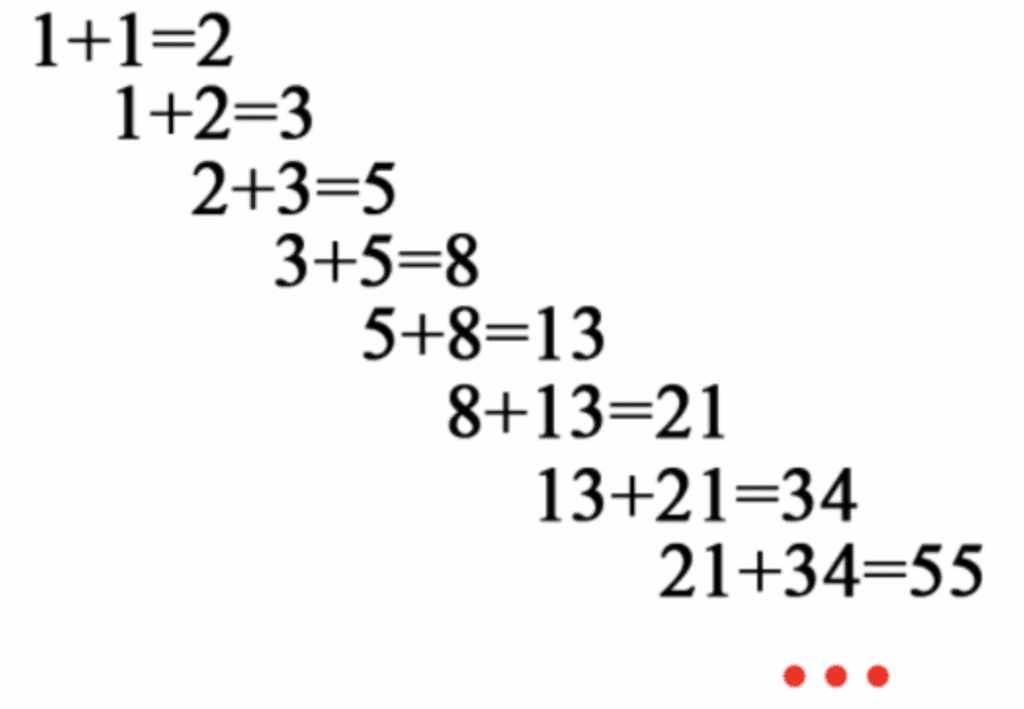
3.4.2. Cài đặt (Phương pháp lặp – Quy hoạch động)

Việc sử dụng đệ quy trực tiếp để tính số Fibonacci thứ n là rất không hiệu quả do phải tính toán lại nhiều lần các giá trị đã biết. Phương pháp lặp (quy hoạch động) hiệu quả hơn nhiều.

def fibonacci(n: int) -> int:
    """
    Tính số Fibonacci thứ n bằng phương pháp lặp.
    Args:
        n: Chỉ số của số Fibonacci cần tính (n >= 0).
    Returns:
        Số Fibonacci thứ n.
    """
    
    if n <= 1:
        return n
    # Khởi tạo hai số hạng đầu tiên
    a, b = 0, 1
    # Lặp từ 2 đến n để tính các số hạng tiếp theo
    for _ in range(2, n + 1):
        a, b = b, a + b
    return b

3.5. Dãy số Catalan

3.5.1. Giới thiệu và ứng dụng

Số Catalan là một dãy số tự nhiên xuất hiện trong nhiều bài toán đếm của toán học tổ hợp. Ví dụ:

  • Số cách đặt n cặp dấu ngoặc đơn hợp lệ. Ví dụ với n=3: ((())), ()(()), ()()(), (())(), (()()). Có 5 cách, và C(3) = 5.
  • Số cây nhị phân có n+1 lá.

3.5.2. Công thức tính toán

Số Catalan thứ n, ký hiệu là C(n), có thể được tính bằng công thức tổ hợp:
C(n) = (1 / (n + 1)) * C(2n, n) = (2n)! / ((n + 1)! * n!)
trong đó C(2n, n) là tổ hợp chập n của 2n.

3.5.3. Cài đặt trên Python (Sử dụng công thức tổ hợp)

import math
def catalan_number(n: int) -> int:
    """
    Tính số Catalan thứ n bằng công thức tổ hợp.
    Args:
        n: Chỉ số của số Catalan cần tính (n >= 0).
    Returns:
        Số Catalan thứ n.
    """
    
    if n < 0:
        return 0
    # Sử dụng math.comb để tính tổ hợp C(2n, n) một cách hiệu quả
    # Yêu cầu Python 3.8+
    c_2n_n = math.comb(2 * n, n)
    # Áp dụng công thức C(n) = C(2n, n) / (n + 1)
    return c_2n_n // (n + 1)

4. Trực quan hóa và gỡ lỗi với Thonny

Để hiểu rõ hơn về cách hoạt động của các hàm trên, học sinh được khuyến khích sử dụng môi trường Thonny IDE. Chức năng gỡ lỗi (debugger) của Thonny cho phép chạy chương trình từng bước và quan sát sự thay đổi giá trị của các biến.

Ví dụ: để gỡ lỗi hàm is_armstrong_number(153):

  1. Đặt một điểm dừng (breakpoint) tại dòng đầu tiên của hàm.
  2. Chạy chương trình ở chế độ gỡ lỗi (Debug).
  3. Sử dụng nút “Step Over” hoặc “Step Into” để đi qua từng câu lệnh.
  4. Quan sát trong cửa sổ “Variables”, các biến s, num_digits, sum_of_powers, digit sẽ được tạo và cập nhật giá trị sau mỗi vòng lặp. Quá trình này giúp trực quan hóa thuật toán tách số và tính tổng lũy thừa.

5. Bài tập vận dụng

5.1. Bài tập 1

5.1.1. Đề bài

Viết chương trình nhận vào một số nguyên dương N (N <= 10000) và in ra tất cả các số hoàn hảo nhỏ hơn hoặc bằng N.

5.1.2. Lời giải và phân tích

Thuật toán rất trực tiếp: ta duyệt qua tất cả các số i từ 1 đến N. Với mỗi số i, ta sử dụng hàm is_perfect_number(i) đã được định nghĩa ở trên để kiểm tra. Nếu hàm trả về True, ta in số i ra màn hình.

# Lời giải cho Bài tập 1
def is_perfect_number(n: int) -> bool:
    # (Sao chép lại mã hàm đã viết ở trên)
    if n <= 1:
        return False
    sum_of_divisors = 1
    for i in range(2, int(n**0.5) + 1):
        if n % i == 0:
            sum_of_divisors += i
            if i * i != n:
                sum_of_divisors += n // i
    return sum_of_divisors == n
def find_perfect_numbers_in_range(limit: int):
    """
    Tìm và in ra các số hoàn hảo trong khoảng từ 1 đến limit.
    """
    print(f"Các số hoàn hảo nhỏ hơn hoặc bằng {limit}:")
    for i in range(1, limit + 1):
        if is_perfect_number(i):
            print(i)
# Ví dụ sử dụng
N = 10000
find_perfect_numbers_in_range(N)

Phân tích: Độ phức tạp của hàm is_perfect_number(i) là O(sqrt(i)). Vì ta gọi hàm này cho mỗi số từ 1 đến N, độ phức tạp tổng thể của chương trình là xấp xỉ O(N * sqrt(N)). Với N = 10000, thuật toán này đủ hiệu quả.

5.2. Bài tập 2

5.2.1. Đề bài

Một “số Fibonacci chính phương” là một số vừa thuộc dãy Fibonacci, vừa là một số chính phương. Viết chương trình tìm tất cả các số Fibonacci chính phương nhỏ hơn 10^12.

5.2.2. Lời giải và phân tích

Ta có thể sinh lần lượt các số Fibonacci. Với mỗi số Fibonacci được sinh ra, ta kiểm tra xem nó có phải là số chính phương hay không. Ta dừng lại khi số Fibonacci vượt quá 10^12.

# Lời giải cho Bài tập 2
import math
def is_perfect_square(n: int) -> bool:
    # (Sao chép lại mã hàm đã viết ở trên)
    if n < 0: return False
    if n == 0: return True
    sqrt_n = int(math.sqrt(n))
    return sqrt_n * sqrt_n == n
def find_square_fibonacci_numbers(limit: int):
    """
    Tìm các số vừa là số Fibonacci vừa là số chính phương nhỏ hơn limit.
    """
    print(f"Các số Fibonacci chính phương nhỏ hơn {limit}:")
    a, b = 0, 1
    while a < limit:
        if is_perfect_square(a):
            print(a)
        a, b = b, a + b
# Ví dụ sử dụng
LIMIT = 10**12
find_square_fibonacci_numbers(LIMIT)

Phân tích: Thuật toán sinh các số Fibonacci rất nhanh. Số lượng số Fibonacci nhỏ hơn 10^12 không lớn (khoảng 60 số). Với mỗi số, ta thực hiện một phép kiểm tra số chính phương có độ phức tạp O(log n) (do sqrt hoạt động trên số lớn). Do đó, thuật toán này cực kỳ hiệu quả. Kết quả thực tế cho thấy chỉ có một vài số thỏa mãn (0, 1, 144).

6. Các lưu ý và lỗi thường gặp

  • Tràn số (Integer Overflow): Trong Python, các kiểu dữ liệu số nguyên có thể lưu trữ các giá trị rất lớn, do đó nguy cơ tràn số thấp. Tuy nhiên, khi làm việc với các ngôn ngữ như C++ hay Java, các phép tính như (2n)! trong công thức Catalan có thể gây tràn số rất nhanh. Cần sử dụng kiểu dữ liệu 64-bit (long long) và các kỹ thuật tính toán trong môi trường modulo khi cần thiết.
  • Hiệu suất của đệ quy: Như đã đề cập với dãy Fibonacci, việc cài đặt công thức truy hồi một cách trực tiếp (đệ quy) thường dẫn đến độ phức tạp hàm mũ và không hiệu quả. Luôn ưu tiên phương pháp lặp hoặc quy hoạch động có nhớ (memoization) để tối ưu.
  • Lỗi làm tròn (Floating-Point Precision): Khi kiểm tra số chính phương, việc so sánh math.sqrt(n) == int(math.sqrt(n)) có thể gặp sai số do cách biểu diễn số thực trong máy tính. Phương pháp int(math.sqrt(n)) * int(math.sqrt(n)) == n được ưu tiên vì nó hoạt động hoàn toàn trên số nguyên và đáng tin cậy hơn.

7. Tổng kết

Bài học đã trang bị các kiến thức nền tảng về một số loại số và dãy số đặc biệt trong Lý thuyết số. Các khái niệm này không chỉ là những công cụ hữu ích để giải quyết các bài toán cụ thể mà còn giúp rèn luyện tư duy chuyển đổi từ định nghĩa toán học sang cài đặt lập trình.

Trong các bài học tiếp theo, các khái niệm này có thể sẽ được sử dụng làm nền tảng để xây dựng các thuật toán phức tạp hơn, đặc biệt trong các bài toán liên quan đến đếm và tổ hợp.

admin
admin
Bài viết: 148

Bài viết liên quan

Để lại một bình luận

Email của bạn sẽ không được hiển thị công khai. Các trường bắt buộc được đánh dấu *